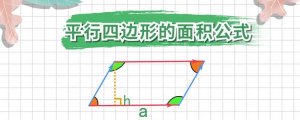
[数学学习]平行四边形的周长公式为C=2(a+b),公式中a、b分别为平行四边形的边长,C为平行四边形的周长。平行四边形的周长是平行四边形的边长的总和。平行四边形,是在同一个二维平面内,由两组平行

四边形内角和等于360°。n边型的内角和为(n-2)×180°,所以四边形内角和为(4-2)×180°=2×180°=360°。
1、四边形的特点:有四条直的边;有四个角。
2、长方形的特点:长方形有两条长,两条宽,四个直角,对边相等。
3、正方形的特点:有4个直角,4条边相等。
4、长方形和正方形是特殊的平行四边形。
5、平行四边形的特点:对边相等、对角相等。
多边形内角和定理证明
证法一:在n边形内任取一点O,连结O与各个顶点,把n边形分成n个三角形.
因为这n个三角形的内角的和等于n·180°,以O为公共顶点的n个角的和是360°
所以n边形的内角和是n·180°-2×180°=(n-2)·180°.(n为边数)
即n边形的内角和等于(n-2)×180°.(n为边数)
证法二:连结多边形的任一顶点A1与其不相邻的各个顶点的线段,把n边形分成(n-2)个三角形.
因为这(n-2)个三角形的内角和都等于(n-2)·180°(n为边数)
所以n边形的内角和是(n-2)×180°.
相关文章
推荐内容